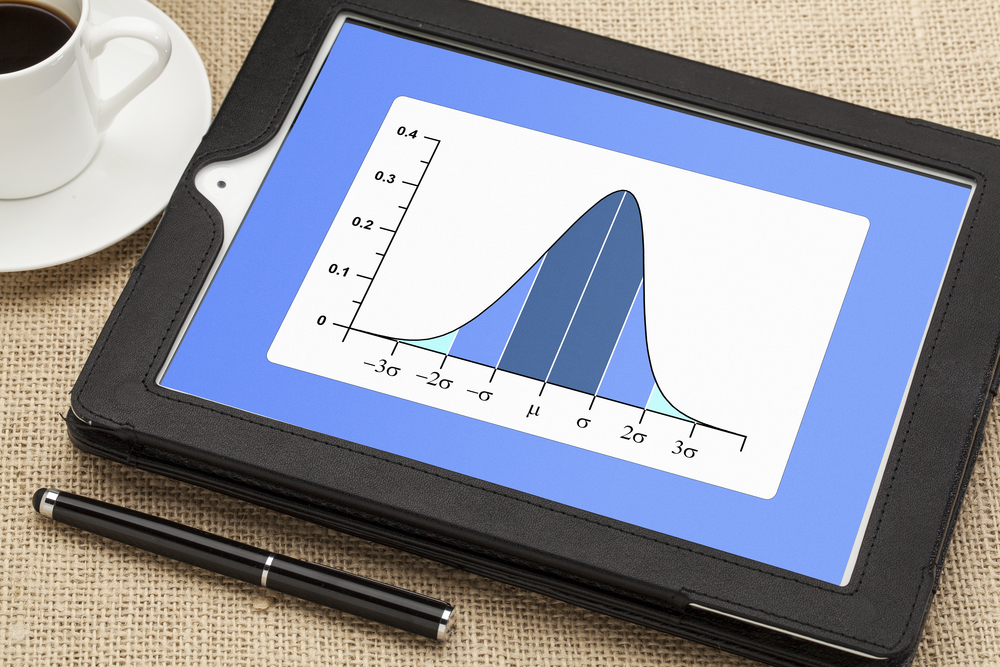
Image: Shutterstock.
Si eres un periodista que lee investigaciones académicas, es probable que hayas visto muchas veces el término “desviación estándar”. Si no estás seguro de lo que significa o de cómo explicárselo al público, sigue leyendo, porque aquí te lo expondremos por partes.
Aquí hay cuatro cosas clave que debes saber.
- La desviación estándar de un conjunto de datos es un número que indica cuánta variación hay dentro de los datos.
Cuando los investigadores analizan datos cuantitativos como tasas de natalidad, las mediciones de temperatura y las puntuaciones de los exámenes de los estudiantes, suelen calcular la desviación estándar de los datos para medir qué tan cerca o lejos están los datos entre sí. Una desviación estándar más alta significa que los datos están más dispersos. Cuanto menor es la desviación estándar, más se agrupan los datos alrededor del valor promedio de los mismos.
Deborah J. Rumsey, profesora de estadística en la Universidad Estatal de Ohio, señala en su libro Estadísticas para Dummies que esta medida proporciona un contexto crucial.
“Sin esto, obtienes solo una parte de la historia de los datos”, escribe. “A los estadísticos les gusta contar la historia del hombre que tenía un pie en un balde de agua helada y el otro en un balde de agua hirviendo. Dijo que, en promedio, ¡se sentía genial! Pero pensemos en la variabilidad de las dos temperaturas de cada uno de sus pies. Un ejemplo más concreto es el precio medio de la vivienda: no te dice nada sobre el rango de precios que puedes encontrar cuando buscas una casa. Es el salario medio puede no no reflejar cabalmente lo que ocurre realmente en tu empresa, si los salarios están muy dispersos”.
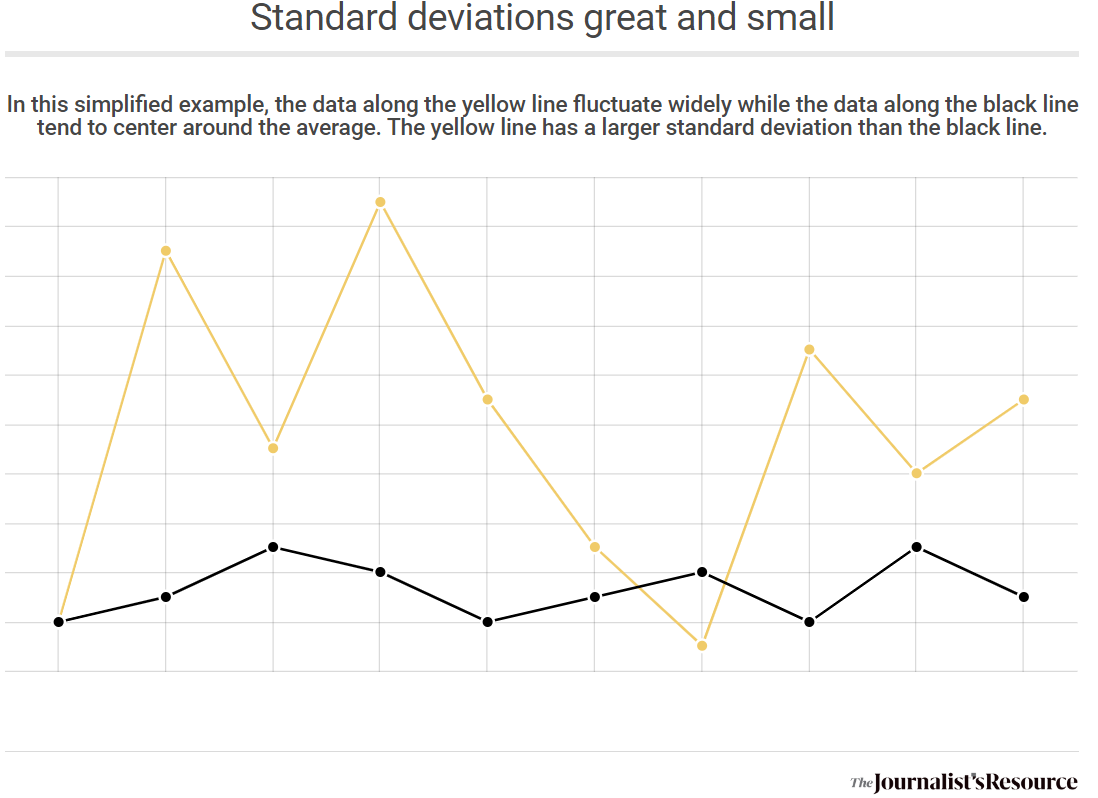
Journalist's Resource
En este ejemplo simplificado, los datos a lo largo de la línea amarilla fluctúan ampliamente, mientras que los datos a lo largo de la línea negra tienden a centrarse alrededor de la media. La línea amarilla tiene una desviación estándar mayor que la línea negra.
- Los científicos pueden usar la desviación estándar para hacer predicciones, investigar tendencias y responder a otras preguntas clave de la investigación.
La desviación estándar de un conjunto de datos desempaña un papel limitado en muchos estudios académicos. Los científicos pueden sólo incluir los valores de desviación estándar en una tabla o lista, o mencionarlos en el cuerpo de un artículo académico.
A veces, sin embargo, los investigadores se basan en esta medida para ayudarlos a responder preguntas centrales de sus estudios. Por ejemplo:
- Los investigadores pueden hacer predicciones sobre el clima, el comportamiento de los votantes, los ingresos fiscales, el uso de la atención médica y muchas otras cosas basándose en parte en la desviación estándar de los datos recopilados a lo largo del tiempo.
- Quienes investigan la renta variable suelen utilizar la desviación estándar de los precios de las acciones para medir la volatilidad del mercado; una desviación estándar alta que indica una alta volatilidad.
- Los investigadores que examinan los resultados de los exámenes de los alumnos pueden usar la desviación estándar para determinar si la mayoría de los estudiantes se rinden en la media o cerca de ella, o si los resultados de las pruebas son desiguales. La medida también permite a los investigadores estimar la proporción de estudiantes que necesitan más ayuda.
Aquí hay una breve explicación de cómo calcular la desviación estándar.
- En algunos estudios, los científicos informan sus resultados en términos de desviaciones estándar en lugar de una unidad de medida, como centímetros o kilos.
Cuando los conjuntos de datos tienen puntos de datos con diferentes unidades, los científicos a menudo necesitan estandarizar o cambiar la escala de los datos antes de establecer comparaciones y buscar relaciones. Por ejemplo, científicos podrían querer examinar la relación entre el consumo de jugo de naranja, medido en onzas (o gramos) y las tasas de vacunación contra la influenza, medidas como el número de vacunas administradas cada mes por cada 100 000 habitantes.
El proceso de estandarización de datos incluye la división de cada punto de datos numéricos por la desviación estándar del conjunto de datos. Al hacer esto se cambian las unidades de medida. En lugar de expresar los hallazgos utilizando unidades comunes como onzas, centímetros y kilogramos, deben expresarse en términos de desviaciones estándar.
Hipotéticamente, los científicos que analizan el consumo de jugo de naranja y las tasas de vacunación contra la influenza podrían concluir que un aumento de una desviación estándar en el consumo de jugo está asociado a una reducción de una desviación estándar en las tasas de vacunación.
Aunque la estandarización de los conjuntos de datos puede facilitar el trabajo de los investigadores, Brian Healy, profesor asociado de neurología en la Escuela de Medicina de Harvard, señala que muchas personas podrían tener dificultades para comprender los resultados. Insta a los periodistas a leer detenidamente estos documentos.
“El problema es que, a menos de se mire muy de cerca el documento, no tendrás idea de lo que significa una desviación estándar que equivalga a uno”, dice Healy.
“Hay que entender las unidades en las que se muestran los resultados”, agrega. “Si se publica un número, hay que asegurarse de entender cómo interpretar el número. Y no se puede entender cómo interpretar el número sin conocer las unidades”.
- Los científicos pueden usar la desviación estándar para ayudar a confirmar si un punto de datos que consideran un valor atípico lo es realmente.
Los valores atípicos son valores extremadamente altos o bajos que pueden complicar los análisis estadísticos y sesgar los resultados. Muchos investigadores eliminan o modifican los valores atípicos causados por un error, por ejemplo, un error al recopilar o ingresar los datos.
Cuando observas un gráfico de todos los datos de un conjunto de datos, algunos puntos de datos parecen ser valores atípicos porque difieren mucho de los demás. Dado que la desviación estándar de un conjunto de datos tiene en cuenta la distancia de los valores individuales con respecto a la media, los científicos suelen utilizarla para evaluar si un punto de datos inusual es un valor atípico. Este método funciona bien para conjuntos de datos que siguen el patrón de una curva simétrica en forma de campana en la que la mayoría de los datos convergen cerca del centro de la campana, donde se encuentra el valor medio.
Tras de calcular la desviación estándar de ese conjunto de datos, es fácil detectar los valores atípicos. Una regla general para los datos que siguen una curva de campana es que aproximadamente el 99,7 % de los datos estarán dentro de tres desviaciones estándar de la media. Los datos que están fuera de ese límite suelen considerarse valores atípicos.
Aunque la desviación estándar de un conjunto de datos se ve afectada por valores atípicos, los periodistas no deben asumir que una desviación estándar grande indica problemas de calidad de los datos. Como escribe Rumsey en Estadísticas para Dummies, “una desviación estándar grande no es necesariamente algo malo; simplemente refleja una gran cantidad de variación en el grupo estudiado”.
Este post fue publicado originalmente por The Journalist’s Resource y se reproduce aquí a través de su licencia Creative Commons. The Journalist’s Resource desea agradecer a Troy Quast, profesor de economía de la salud en la Facultad de Salud Pública de la Universidad del Sur de Florida, y a Brian Healy, profesor asociado de neurología en la Facultad de Medicina de Harvard, por su ayuda en la elaboración de estos consejos.
 Denise-Marie Ordway es la gerente editorial de The Journalist’s Resource desde 2015. Se unió al equipo luego de trabajar para periódicos y estaciones de radio en Estados Unidos y Centroamérica. Su trabajo ha sido publicado por USA Today, The New York Times y el Washington Post. Fue becaria Harvard-Nieman en 2014-15.
Denise-Marie Ordway es la gerente editorial de The Journalist’s Resource desde 2015. Se unió al equipo luego de trabajar para periódicos y estaciones de radio en Estados Unidos y Centroamérica. Su trabajo ha sido publicado por USA Today, The New York Times y el Washington Post. Fue becaria Harvard-Nieman en 2014-15.
